Este poliedro regular convexo está formado por doce caras, que son pentágonos regulares, veinte vértices y treinta aristas. De cada arista parte otro pentágono que es opuesto diametralmente. Con lo que cada cara del dodecaedro tiene la opuesta paralela y girada 180º.

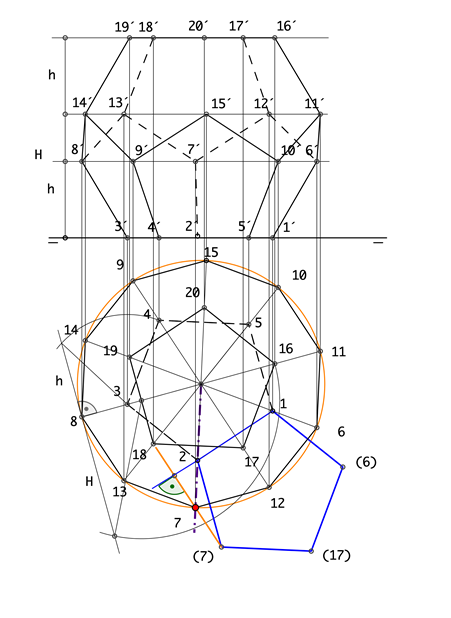
Comenzamos colocando el pentágono regular de base, ya que está contenido en el PH, para hallar los demás vértices del sólido y teniendo en cuenta lo mencionado unas líneas más arriba, se abate el pentágono que tiene por arista común la 1-2,  se traza desde (7) abatido una perpendicular a la arista 1-2 donde corta perpendicularmente a la unión del centro del pentágono con 2 estará el punto 7, los demás vértices que se encuentra a la misma altura se dibujan sobre la circunferencia trazada con radio O-7. Por último queda dibujar la cara superior, que será otro pentágono situado sobre el inferior pero girado 180º. El contorno aparente en proyección horizontal como podemos observar es un decágono.

Para hallar la proyección vertical es necesario conocer dos cotas H, h; a la que se encuentran los vértices.
Una de ellas, por ejemplo la H se corresponde con el cateto de un triángulo rectángulo en el que la hipotenusa es la apotema del pentágono y el otro cateto la proyección de ésta.  A esta altura se dibujan los vértices 11, 12, 13, 14, 15.
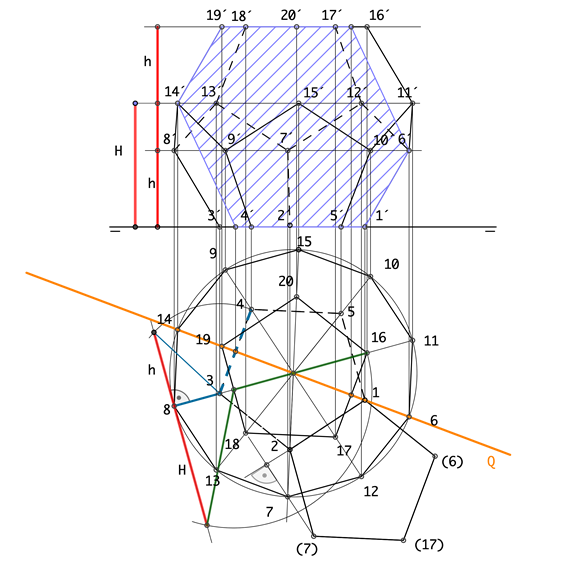
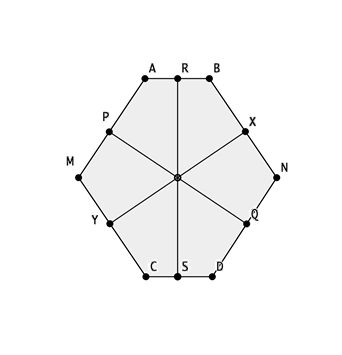
La otra altura, h, es un cateto de un triángulo rectángulo en el que la hipotenusa es una de las aristas del poliedro y el otro cateto la proyección de esa arista. Los vértices que tienen esa altura serán 6, 7, 8, 9, 10.
Los vértices perteneciente a la cara superior están sobre la altura H+h.

El plano proyectante horizontal, K (K´-K) contiene a los vértices (1, 6, 14, 19), se procede a realizar la sección y una vez trazado el polígono resultante se abate sobre el vertical de proyección el resultado es un hexágono que tiene dos lados opuestos iguales al valor de la arista y los otros cuatro son alturas de las caras o apotemas. Procedemos a explicar las distancias que en ella se encuentran:

• Arista =AB =CD
• Altura de caras =AM = BN =CM=DN
• Ángulo formado por dos caras consecutivas=AMD
• C=BND
• Diagonal =AD=BC=diámetro de esfera circunscrita
• Distancia entre aristas opuestas =RS=diámetro de la esfera tangente a las aristas
• Distancia entre caras opuestas=PQ=XY= diametro de la esfera inscrita tantente a las caras

RECUERDA:

Las secciones están contenidas en los planos y a menos que estos sean paralelos a uno de los planos de proyección su forma no se encuentra en verdadera magnitud, para poder situar la sección en verdadera magnitud es necesario utilizar uno de los métodos estudiados, en estos caso abatiremos hacia el horizontal o el vertical de proyección.