| ICOSAEDRO | |
El icosaedro es el último de los poliedros platónicos, consta de veinte caras con forma de triángulos equiláteros, treinta aristas y doce vértices. |
|
| Icosaedro con una diagonal vertical | |
Para la construcción del icosaedro es importante tener en cuenta que de cada vértice parten cinco aristas. Y sabiendo que éste se encuentra con una diagonal perpendicular al plano horizontal, con lo que diez de sus aristas están sobre un plano paralelo al horizontal, lo tendremos en esa proyección representado por dos pentágonos invertidos, uno con respecto al otro y de lado igual al de la arista del poliedro, siendo su contorno aparente un decágono formado por la unión de cada uno de los vértices de los pentágonos. Para terminar de dibujar esa proyección basta con unir el centro de los pentágonos con los vértices. La proyección vertical se obtiene por el mismo proceso que en el dodecaedro por triángulos rectángulos |
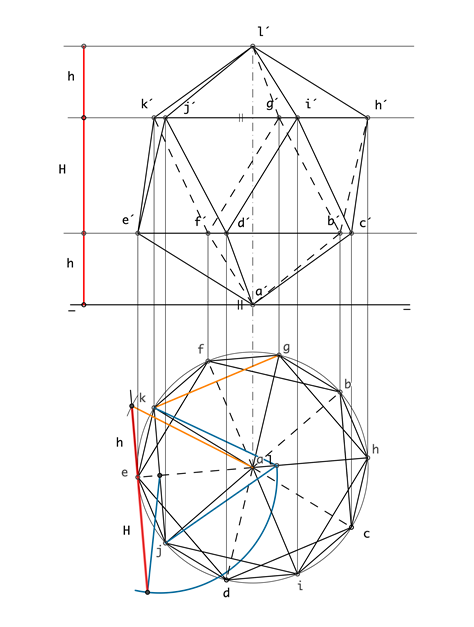 |
RECUERDA: H se corresponde con el cateto de un triángulo rectángulo en el que la hipotenusa es la apotema del triángulo (cara del icosaedro) y el otro cateto la proyección de éste. |
|
| Sección principal de Icosaedro | |
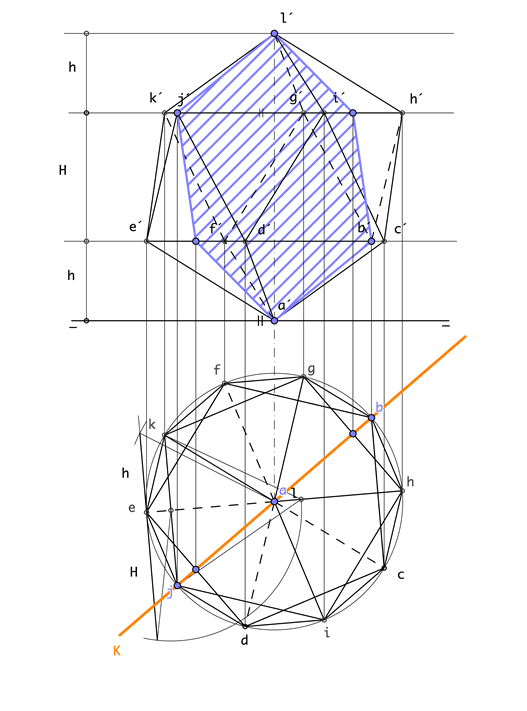
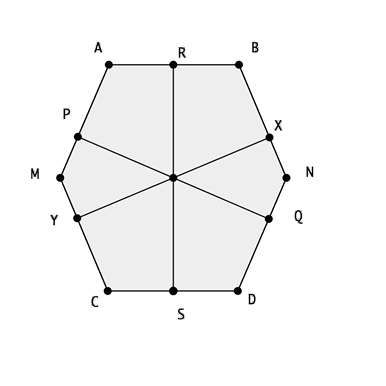
Para cortar el icosaedro según la sección principal se sitúa apoyado en un vértice y con la diagonal que contiene este vértice vertical sobre el horizontal de proyección. El plano secante será proyectante horizontal y contendrá a dos aristas opuestas las cuales son paralelas. Una vez hallada la sección observamos que ésta en verdadera magnitud es un hexágono irregular que tiene al igual que el dodecaedro dos lados de la misma logitud que las aristas del poliedro, y las otras cuatro son apotemas de las caras del sólido. A continuación procedemos a analizar la sección:
|
 |
 |
|