Prámide

PIRÁMIDE

La pirámide es una superficie piramidal limitada en un sentido por un punto propio y en el otro por un plano secante.

La superficie piramidal es una superficie radiada formada por una generatriz que pasa por un punto fijo, denominado vértice y se apoya sobre un polígono, siendo éste su directriz. La directriz se forma por el plano secante que corta a todas las generatrices del sólido.

Elementos de una pirámide

Aristas laterales: perteneciente a la superficie piramidal son los que unen el vértice con la base
Aristas básicas: producida al cortar el plano a las aristas laterales
Caras laterales: son los triángulos formados por las caras de la pirámide tienen todos, un vértice común.
Base: es la cara contenida en el plano secante ya sea regular o irregular.
Altura: la distancia existente entre la base y el vértice de la pirámide.

Clasificación

Pirámide recta/oblicua: Una pirámide es recta cuando el eje es perpendicular a la base, una pirámide será oblicua cuando la altura en proyección, no coincide en el centro de la misma.
Pirámide regular/irregular: Una pirámide es regular cuando es recta y el polígono que forma su base es regular, siendo irregular la pirámide cuando el polígono se su base es irregular.
Pirámide truncada: Es aquel resultante de la intersección de un plano con el sólido pero sin cortar a la base.

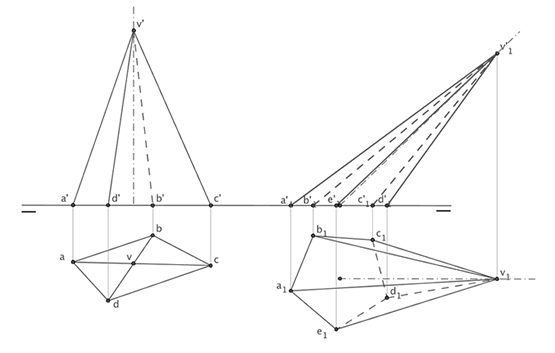
Proyecciones diédricas de una pirámide

Como ya hicimos mención en el caso anterior las proyecciones de la pirámide sobre los planos de proyección viene dada por su contorno exterior o aparente y las rectas o aristas que se encuentran dentro de ella. Al estar la pirámide contenida en el plano de proyección horizontal, su proyección sobre este plano estará formado por el polígono base y las proyección en planta de las aristas unidas con el vértice.

La proyección vertical será el triángulo formado por el conjunto de aristas vistas y ocultas dependiendo de su posición respecto del contorno aparente.

Sección, desarrollo y transformada de una pirámide

En este caso hemos optado por seccionar la pirámide con un plano oblicuo, siendo la pirámide recta e irregular.

Como ya sabemos el ejercicio queda resuelto cuando hallemos la sección del cuerpo con el plano, para ello hay que hallar las intersecciones de todas sus aristas con el plano dado. Por último tendríamos que unir todos los puntos de esas intersecciones y abatirla para obtener su verdadera magnitud.

Para resolver este problema podemos emplear dos métodos:

1º método: Consiste en contener cada una de las aristas de la pirámide en planos proyectantes y hallar su intersección. Para facilitar el ejercicio podremos utilizar un único plano proyectante, una vez obtenido el punto de intersección se continúa el ejercicio por afinidad.

*Si la traza horizontal del plano cortase a alguna de las aristas básicas de la pirámide, estos son considerados puntos de sección y se sitúan en proyección vertical sobre la LT, por estar contenidos en el plano horizontal de proyección.

2º método: En este caso se realiza un cambio de plano que convierta el plano dado en uno proyectante, también se cambia la pirámide. Una vez obtenidas las nuevas proyecciones se procede ha realizar la sección.

Por último se halla la verdadera magnitud de la sección abatiendo el plano que la contiene.

Proyecciones diédricas de una pirámide cuando se encuentra apoyada en planos diferentes a los de proyección

Para apoyar una pirámide sobre un plano oblicuo:

Empezaremos conteniendo la base de la pirámide en el plano, para ello utilizamos las rectas notables del plano por su sencillez.
Hallamos el centro desde donde se levanta la altura, que en este caso es el circuncentro del triángulo base, abatiendo la base sobre unos de los planos de proyección.
Desabatimos o reintegramos el centro hallado y trazamos perpendiculares desde dicho punto a las trazas del plano, ya que es una pirámide recta.
Para llevar la altura sobre su eje primero deberemos situar dicha recta de manera que podamos trabajar en verdadera magnitud, es decir, girar la recta para situarla horizontal o frontal; o utilizar el método de distancia entre puntos.
Sobre la recta girada llevamos la medida real que en este caso es de unos 7 cm, para luego deshacer el giro.
Una vez hallado el vértice (punto de altura de la pirámide) en proyección, se une con cada unos de los vértices de la base.
Por último se dibujan las aristas vistas y ocultas de la figura.