Cono

CONO
La superficie cónica es una superficie radiada engendrada por una recta generatriz que gira alrededor de un punto fijo llamado vértice y apoyándose sobre una curva plana denominada directriz. Por lo general esta curva plana es una circunferencia pero también puede ser una curva hiperbólica, parabólica, elíptica etc.
Elementos de un cono
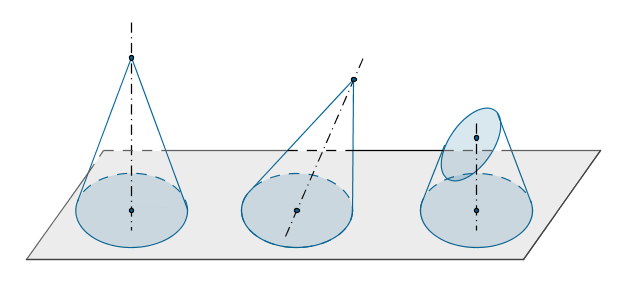
Generatriz: recta que da forma al sólido Base: figura plana contenida en el plano secante que adopta la forma de la directriz Eje: recta alrededor de la cual gira la generatriz Altura: Es el segmento resultante de trazar una perpendicular a la base desde el vértice
Clasificación
El cono puede ser considerado una pirámide de infinitas caras o aristas ya que su generatriz gira constantemente alrededor de un eje pasando por infinitos vértices. Cono recto u oblicuo: el sólido queda definido con el conocimiento de la base y su altura. Si el eje es perpendicular al plano que contiene a la directriz y por lo tanto a la base, éste se considera recto; si por lo contrario el eje es oblicuo a dicho plano, el cono recibe el nombre de oblicuo. Cono de revolución:* recordando lo que dijimos al principio, un cono será de revolución cuando la generatriz que gira alrededor del eje mantiene la misma inclinación, o sea, cuando el ángulo formado por dicha generatriz y el eje es constante. Cono truncado: se llama cono truncado al resultado de seccionar un cono por un plano secante ya sea este paralelo a la base o no pero sin cortarla.

Proyecciones diédricas de un cono
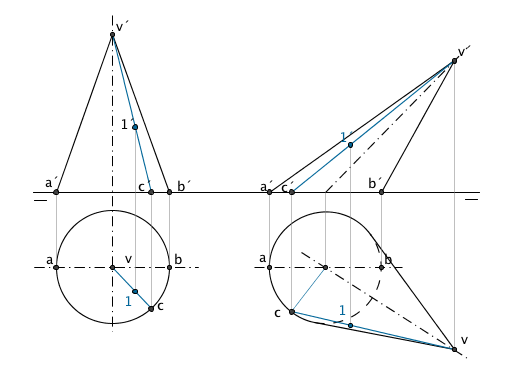
De las posibles representaciones de un cono la que más utilidades nos muestra es, el cono recto de revolución. Su directriz será una circunferencia contenida en el plano horizontal de proyección; la proyección vertical del sólido es un triángulo isósceles cuyos lados iguales corresponde a la generatriz del cono siendo éste su contorno aparente, la base de dicho triángulo está contenida en la LT y tiene la misma medida que el diámetro de la circunferencia que se proyecta en el plano horizontal. Las generatrices del contorno aparente son rectas frontales con lo que se encuentran en verdadera magnitud. Para representar un cono oblicuo que no sea de revolución (base circular) basta conocer su altura, ya que el contorno aparente se define uniendo en el vertical, el vértice del cono con la proyección en LT de los puntos extremos de su base y en el horizontal trazando rectas tangentes desde el vértice a la circunferencia.

IMPORTANTE: para que un punto pertenezca al cono tiene que tener sus proyecciones 1´-1 contenidas en una generatriz c´-c del cono
Sección, desarrollo y transformada de un cono
La sección de un cono de revolución por un plano secante da como resultado una curva cónica. Dependiendo de la posición del plano secante con respecto a la generatriz y al eje del cono obtendremos un círculo, una elipse, una parábola o una hipérbola. Si el plano es perpendicular a la generatriz la sección obtenida es una circunferencia. Si el plano secante es oblicuo a la generatriz y al eje del cono la sección será una elipse. Si situamos el plano paralelo a una de las generatrices del sólido la sección resúltate será una parábola. Cuando el plano secante es paralelo a dos generatrices la curva será una hipérbola. Los métodos empleados para hallar la sección en esta superficie radiada, son los mismos que la pirámide: por intersección de generatrices con el plano secante o cambio de plano. En la figura se muestra un ejemplo de sección por un plano proyectante

						Pág. 1		Página 0