CILINDRO

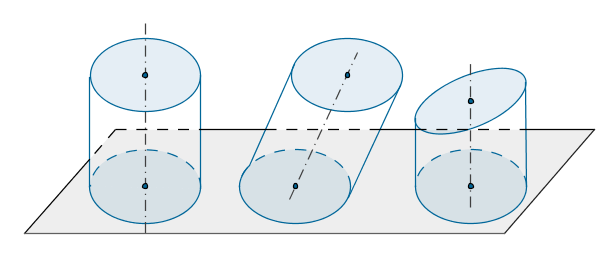
El cilindro es una superficie radiada formada por una recta, que apoyándose sobre una curva, se traslada de forma constante y paralela a sí misma o al eje central.
La superficie cilíndrica se encuentra limitada por dos planos secantes, paralelos entre sí y que contienen a las bases del cilindro.

Podríamos considerar el cilindro como un prisma de infinitas caras o aristas.

• Cilindro recto: cuando la generatriz es perpendicular a la base el cilindro será recto, de lo contrario oblicuo.
  
  
• Cilindro de revolución: cuando la generatriz equidista del eje el cilindro se denomina de revolución. Las bases son por lo tanto círculos en el caso de que sea recto o elipses si es oblicuo. Si el cilindro no es de revolución su base puede ser cualquier curva cerrada y plana.
  
  
• Cilindro truncado: este cilindro se forma cuando el plano que lo corta en su parte superior no es paralelo al inferior.

Siendo el cilindro que vamos a representar en proyecciones diédricas recto y de revolución, apoyado sobre el plano horizontal. Tendrá como proyección horizontal una circunferencia en verdadera magnitud, de radio igual a la distancia de la generatriz al eje. Su proyección vertical es un rectángulo que vendrá dado por las dos generatrices exteriores paralelas a este plano y perpendicular a la LT.

Si el cilindro fuese oblicuo y paralelo al vertical tendría como base una elipse y las generatrices que se proyectan en el plano vertical formarían el mismo ángulo con la LT que la generatriz del cilindro con su base, por ser su proyección una recta frontal.

Cilindro apoyado en un plano que corta o contiene a la LT.

Para hallar la sección que produce un plano secante en un cilindro se pueden utilizar los mismos métodos que hemos empleado en las demás superficies radiadas, estos son por intersecciones utilizando planos proyectantes que contengan a las generatrices, por afinidad o por cambio de plano.

IMPORTANTE: el plano secante se puede situar paralelo, perpendicular u oblicuo al eje. Si el cilindro es de revolución las secciones producidas por estos planos serán: un paralelogramo si el plano se sitúa paralelo al eje, una circunferencia si éste es perpendicular a eje y una elipse si se sitúa oblicuo. No obstante los casos más frecuentes son de planos oblicuos al eje.

Dado el cilindro de revolución y el plano secante P (P´-P) por sus proyecciones diédricas, vamos a proceder a la realización del ejercicio utilizando varios planos proyectantes que contengas a las generatrices del sólido.
Si se quisiera hacer por cambio de plano, basta con cambiar el vertical transformando el plano oblicuo en uno de canto y situar luego, el sólido en su nueva posición. La sección se obtiene directamente sobre la traza vertical del plano, hallamos la proyección horizontal de cada uno de los puntos de la sección, llevándolos a su generatriz correspondiente.