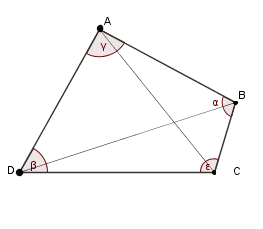
Figura plana y cerrada compuesta por una recta quebrada que empieza y acaba en el mismo punto haciendo cuatro ángulos. Se denomina vértices a los puntos donde la recta quebrada cambia de dirección y lado, al segmento comprendido entre cada dos vértices.

La figura nos muestra la nomenclatura utilizada.

Propiedades

• Los ángulos internos de un cuadrilátero siempre suman 360º

• Si la suma de los lados opuestos de un cuadrilátero es la misma, el cuadrilátero será circunscriptible, es decir, que puede circunscribir a una circunferencia. AB + CD = BC + AD

• Cuando los ángulos opuestos de un cuadrilátero suman 180º (sumplementarios), el cuadrilátero podrá ser inscriptible, es decir qeu puede inscribirse a una circunferencia.

• Al unir los puntos medios de los lados de cualquier cuadrilátero como resultado obtenemos un paralelogramo

Para comprobar que se cumplen las propiedades descritas mueve los puntos rojos

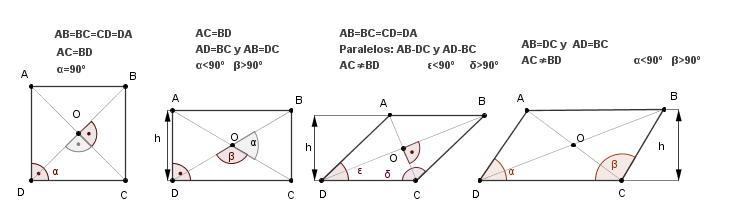
Paralelogramos

Son aquellos cuadriláteros que tienen sus lados paralelos dos a dos

• Cuadrado. Sus lados son iguales y paralelos dos a dos. Todos sus ángulos son rectos. Sus diagonales son perpendiculares entre sí y se bisecan*

• Rectángulo. Tienen lados iguales y paralelos dos a dos. Todos sus ángulos son de 90º. sus diagonales son iguales, pero no perpendiculares y se bisecan, como hemos dicho con ángulos diferentes a 90º.

• Rombo. Tienen todos sus lados iguales y paralelos dos a dos. Sus ángulos son iguales dos a dos. Las diagonales no tienen la misma medida pero se bisecan perpendicularemente.

• Romboide. Tienen lados y ángulos iguales dos a dos. Sus diagonales son desiguales, oblicuas y se bisecan formando ángulos diferentes a 90º.

*Bisecar: Dividir en dos partes iguales. Por lo tanto dos diagonales que se bisecan quiere decir que se cortan en su punto medio.

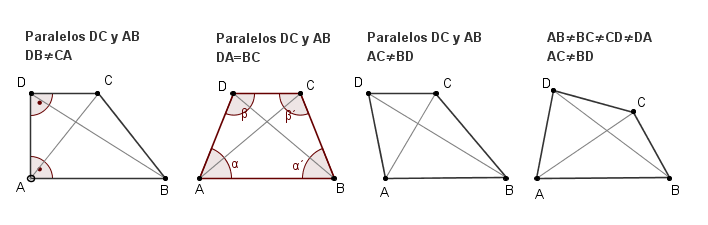
Los trapecios son cuadriláteros que tienen dos lados paralelos a los que se les denomina lados básicos

• Rectángulo. El trapecio rectángulo tienen sus lados básicos paralelos y dos ángulos rectos. Las diagonales son de diferente medidas, oblicuas y no se bisecan.

• Isósceles. Trapecio que tiene los lados laterales iguales y forman el mismo ángulo con los lados básicos. Las diagonales son de la misma medida, oblicuas y no se bisecan.

• Escaleno. Trapecio que tiene todos sus ángulos y lados desiguales. Sus diagonales son de medidas diferentes, oblicuas y no se bisecan.

Son aquellos cuadriláteros que no tienen ningún lado paralelo, por tanto sus lados y ángulos son de diferente medidas