| TRIÁNGULOS |
| Definición |
| Podemos definir triángulo como la
superficie plana y cerrada formada por tres rectas que se cortan dos a dos. La
intersección de estas rectas dan lugar a los vértices del triángulo y a los lados, que
son los segmentos comprendidos entre los vértices. |
| Como sabes podemos dar más de una definición a un mismo concepto
geométrico. Por ejemplo, otra definición de triángulo puede ser la de
superficie plana formada por una recta quebrada que empieza y termina en el mismo punto
haciendo tres ángulos. |
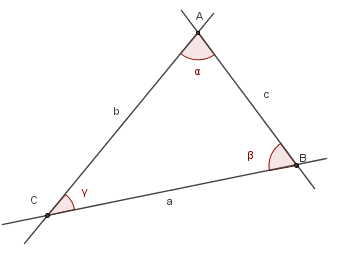
| Notaciones En dibujo técnico se utiliza una nomenclatura concreta para designar los
diferentes elementos del triángulo.
Observa el dibujo a la izquierda. |
 |
| Propiedades Una de las propiedades más importantes de los
triángulos es que los ángulos internos suman siemtre 180º y como consecuencia de
este hecho se deduce que:
- Un triángulo nunca puede estar formado por más
de un ángulo recto u obtuso
- Cualquiera de los lados de un triángulo, es
mayor a la diferencia de los otros dos lados y menor a la suma de estos
- En un triángulo rectángulo los dos ángulos
agudos son complementarios, es decir, suman 90º
- En un triángulo rectángulo la hipotenusa es
mayor que los otros dos lados.
|
Desliza los
puntos rojos, para comprobar que las propiedades mencionadas arribas se cumplen. |
|
|
| Igualdad y semejanza entre
triángulos |
Dos
triángulos serán iguales si se cumplen una de las siguientes condiciones:
- Si tienen los tres lados iguales
- Cuando tienen iguales dos lados y el ángulo
comprendido entre ellos
- Cuando tienen iguales dos ángulos y un lado
|

|
Dos triángulos serán semejantes cuandocumpla una de las
siguientes condiciones:
- Cuando tengan sus lados proporcionales
- Cuando tenga un ángulo igual y los lados que lo
forman sean proporcionales
- Cuando tiene dos ángulos iguales y los tres
lados proporcionales
|

|
| CLASIFICACIÓN DE TRIÁNGULOS |
Por su configuración
Rectilíneos. Todos
sus lados son líneas rectas
Curvilíneos. Todos
sus lados los componen curvas
Mixtilíneos. Es
el triángulo en que sus lados los forman rectas y curvas
|
|
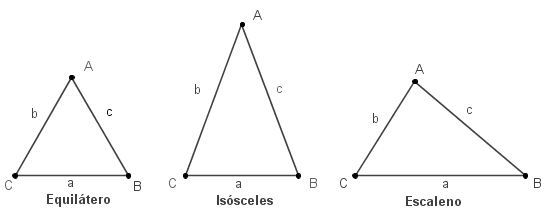
Atendiendo a las medidas de
sus lados
Equilátero. Tienen
todos sus lados iguales
Isósceles. Triángulo
que tiene dos lados iguales y uno desigual
Escaleno. Tiene
todos sus lados desiguales
|
|
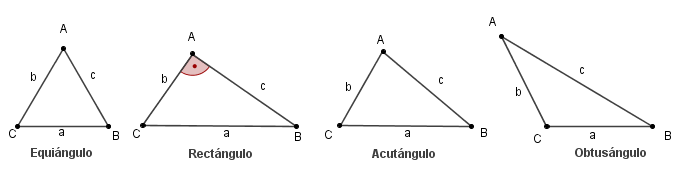
Atendiendo a las medidas de
sus ángulos
Equiángulo. Triángulo
que tiene todos sus ángulos iguales
Rectángulo.
En el caso de que el triángulo tenga un ángulo recto
Acutángulo. Cuando
los tres ángulos de un triángulo son agudos
Obtusángulo. Uno
de los ángulos del triángulo es agudo
|

|
| RECTAS
Y PUNTOS NOTABLES DE UN TRIÁNGULO |
Todos los triángulos tienen cuatro direcciones notables.
Circuncentro y
mediatrices. Para hallar el circuncentro de un triángulo, basta trazar las
mediatrices de cada uno de los lados. El circuncentro es el centro de la circunferencia
circunscrita al triángulo. Con lo que podemos definir el circuncentro como el
lugar geométrico de los puntos del plano que equidistan de los vértices de un
triángulo. El circuncentro estará dentro del triángulo si este es acutángulo,
fuera si es obtusángulo y en la mitad de la hipotenusa si es rectángulo.
Incentro y
bisectrices. Las bisectrices de un triángulo son las rectas que pasando por cada
uno de sus vértices dividen al ángulo de cada uno de ellos en dos partes iguales, dando
lugar en su corte al incentro. El incentro es el centro de la circunferencia inscrita al
triángulo, por lo tanto, esta circunferencia será tangente a cada uno de los lados del
mismo.
Ortocentro y alturas. Las
alturas de un triángulo son las rectas perpendiculares trazadas desde un vértice al lado
contrario. Las tres alturas se cortan en un msimo punto llamado ortocentro. Si unimos los
pies de las tres alturas obtendremos el triángulo órtico. El
ortocentro puede quedar dentro del triángulo, fuera o coincidente en un vértice del
mismo como sucede con el triángulo rectángulo.
Baricentro y medianas.
Las medianas de un triángulo son las rectas que unen cada vértice con el punto
medio del lado contrario. El corte de esas tres rectas dan como resultado el baricentro;
centro de gravedad del triángulo. Este punto se encuentra a 1/3 del punto medio del lado
y a 2/3 del vértice. Al unir los puntos medios de cada lado obtenemos el triángulo
complementario, semejante al anterior en una homotecia de razon -1/2 y centro el
baricentro
|
Deslizando los puntos rojos podrás cambiar la forma de
los triángulos |
|
|
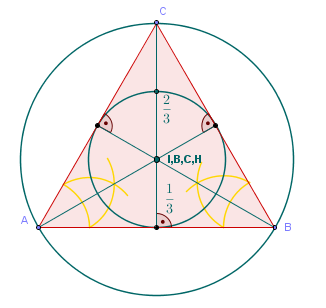
| ATENCIÓN: En el triángulo equilátero todos los centros
coinciden en un mismo punto, por ser un polígono regular (tiene todos sus lados y
ángulos iguales) |
 |
|
|
|





