Pág. 2

Pág. 3

Página 1

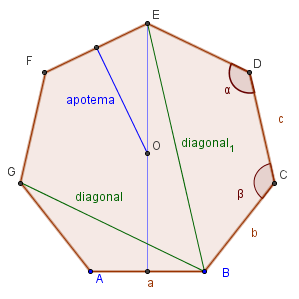
Definición

Un polígono regular convexo, es una figura plana compuesta por lados y ángulos inguales, es decir, que se puede inscribir dentro de una circunferencia.
Los elementos de un polígono regular convexo son:

• Vértices: A, B, C, D...

• Lados: AB, CD, EF, o bien a, b, c, d, e...

• Ángulos:Â, o a

• Diagonales: Son las rectas que unen dos vértices no consecutivos. Los únicos polígonos que poseen sus diagonales iguales.

• Apotema: Es la recta que une el centro del polígono con el punto medio de cualquier lado. La apotema coincide con el radio de la circunferencia inscrita al polígono.

• Centro del polígono: Es el punto interior del polígono, con lo que equidista de todos los vértices del mismo. El segmento que une el centro con cualquier radio del polígono es el rado de la circunferencia circunscrita.

Algunas de las propiedades de los polígonos convexos son:

• Un polígono convexo se puede descomponer en tantos triángulo como lados tenga menos dos.

• La suma de los ángulos internos de un polígono es igual al producto de 180º por el número de lados menos dos

• El valor de la suma de los ángulo externos de un polígono es de 360º.

• El valor del ángulo central de un polígono regular se halla dividiendo 360º entre el número de lados que lo forman.

• El número de las diagonales de un polígono se calcula multiplicando el número de lados por el número de lados menos tres, dividiendo el resultado entre dos.

• En un polígono regular de un número impar de lados la mediatriz de un lado coincide con el vértice opuesto; en un polígono de un número par de lados la mediatriz de un lado coincide con la del lado opuesto.

Para construir un polígono regular conocido el radio de la circunferencia circunscrita basta con dividir dicha circunferencia en tantas partes iguales como lados tenga el polígono. Hay dos métodos para construir este tipo de polígono; uno general con el que podremos dibujar cualquier polígono inscrito en una circunferencia y otro específico.

Por su rapidez y su sencillez, siempre que se pueda, emplearemos los métodos particulares para el trazado de los polígonos.

1º Sobre una circunferencia de radio r y centro O, se traza un diámetro cualquiera (AD).

2º Con centro en D y radio r se dibuja un arco que corta a la circunferencia en los vértices B, C del triángulo inscrito en ella.

3º Unimos A,  B y C para dibujar el polígono.

4ª Para construir el hexágono pinchamos en el vértice contrario a D, A y hacemos un arco con radio r. Los puntos obtenidos en el corte del arco con la circunferencia serán los dos vértices que faltan para dibujar el hexágono.

5º Si trazamos las mediatrices de cada uno de los lados del hexágono, (también se pueden trazar perpendiculares desde el  centro de la circunferencia a los lados del hexágono) dividiremos la circunferencia de manera que al unir esas divisiones con los vértices del hexágonos obtenemos un polígono con el doble número de lados.

El hexágono es el único polígono regular que tiene el lado y el radio de la circunferencia circunscrita a él   iguales.

Pág. 2

Pág. 3

Página 1