|
ELIPSE |
| Definición |
| La elipse es una curva cerrada y plana. Se define como el lugar geométrico de los puntos del plano, cuya suma de distancias, de cada uno de ellos a otros dos fijos, denominados focos(F-F') es una constante, siendo igual al eje mayor (A-B) |
Elementos de la elipse |
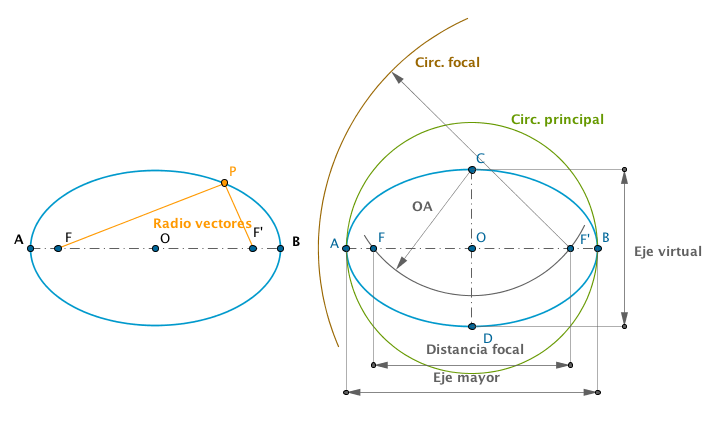
Los elementos más importantes para la configuración de la elipse son:
- Ejes. La elipse tiene dos ejes de simetría uno mayor (AB) y otro menor (CD) que se cortan en su punto medio, denominado centro de la elipse. El eje mayor lo conocemos con el nombre de eje principal o mayor y eje menor, secundario o virtual
- Focos. Se denominan como F y F´, están situados sobre el eje principal de la curva. Para obtener su posición sobre dicho eje se hace un arco desde cualquiera de los extremos del eje menor con radio OA (semieje principal).
- Distancia focal. Es la distancia que existe entre los focos.
- Radio Vectores. Son las rectas que unen un punto cualquiera de la curva con los focos.
- Circunferencia principal. Es la trazada desde el centro con radio el semieje real. Se podría definir como lugar geométrico de los pies de las perpendiculares trazados desde un foco a las tangentes de la elipse.
- Circunferencia focal. Es la circunferencia trazada desde los focos con radio el eje mayor. Como la elipse tiene dos focos, se podrán trazar dos circunferencias focales una desde cada foco. Es el lugar geométrico de los puntos simétrico de un foco respecto de las tangentes
|
 |
| Construcción de la elipse |
| Por puntos |
Dados los ejes de la elipse y los focos.
1º Dividimos en un número de partes iguales la distancia de F a O, es decir la semidistancia focal.
2º Se realizan arcos con centro en F y F´ y radio A1. Tras realizar esta operación se dibujan otros dos arcos desde los mismos centros con radio B1, al observar veremos que los arcos realizados se cortan en una serie de puntos. Estos puntos pertenecen a la curva que queremos dibujar.
3º Realizamos la misma operación pero con radio igual A2, A3… y B2, B3… hasta completar todas las divisiones que hicimos en principio.
4º Por último unimos todos los puntos a mano alzada o con plantilla, para obtener la elipse. |
|
| Por haces proyectivos o intersección de rectas |
Dado los dos ejes de la cónica.
1º Dibujamos un rectángulo cuyos lados tengan la misma medida que los ejes de la elipse.
2º Dividimos el eje mayor de la elipse y los dos lados menores del rectángulo en el mismo número de partes.
3º Trazamos rectas que unan los extremos C y D con las divisiones del eje mayor de la elipse y con las divisiones que hicimos en los lados del rectángulo.
4º Las intersecciones de las rectas que contienen puntos homólogos (C1-D1, C2-D2, C3-D3…) serán puntos de la curva.
5º Solo nos queda unir todos los puntos hallados para trazar la elipse.
|
|
|
Por afinidad o circunferencias concéntricas |
Conocidos los ejes de la elipse.
1º Dibujamos dos circunferencias concéntricas una con diámetro el eje mayor y otra con diámetro el eje menor.
2º Se trazan varios diámetros que corten a las dos circunferencias.
3º Por los extremos de los diámetros de la circunferencia mayor se hacen rectas perpendiculares al eje mayor, y por los diámetros de la circunferencia de eje menor, se trazan rectas paralelas al eje mayor. Estas rectas se cortarán en puntos de la curva.
4º Dibujamos la curva igual que en los casos anteriores, a mano alzada o con plantilla. |
|
| |
|
|
|
|
|
