|
HIPÉRBOLA |
| Definición |
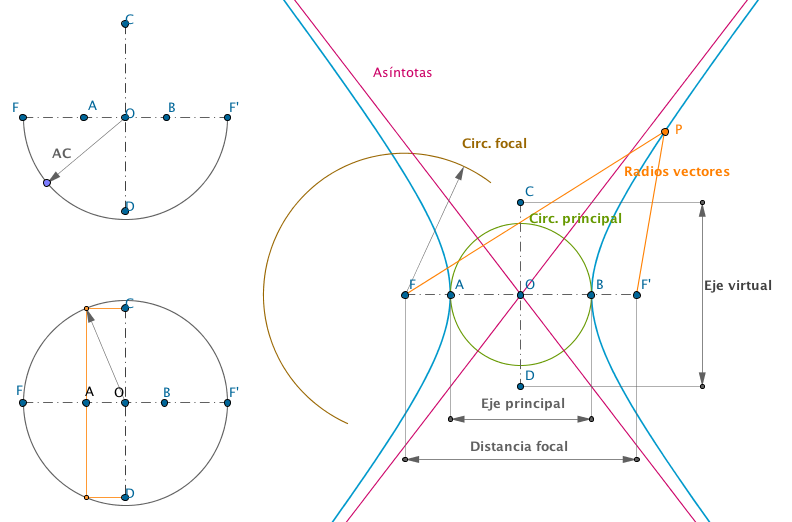
| La hipérbola es una curva plana y abierta compuesta por dos ramas y se define como el lugar geométrico de los puntos del plano cuya diferencia de distancias de cualquier punto de la curva a otros dos fijos, llamados focos (F-F'), es una medida constante igual el eje principal. |
| Elementos de la hipérbola |
-
Ejes. La hipérbola tiene dos ejes de simetría el principal, (AB) y el eje imaginario, (CD); estos ejes son perpendiculares entre sí en el punto medio de la curva, también denominado centro de la hipérbola.
-
Focos. Los focos están situados en el eje real, estos dos puntos se identifican con la letra F y F´. Como son puntos fijos de la curva se pueden hallar haciendo centro en (O) (punto medio de la hipérbola) y radio AC(uno de los extremos del eje imaginario).
-
Distancia focal. Es la distancia que hay entre los focos.
-
Radios vectores. Son las rectas que unen cada punto de la curva con los focos.
-
Circunferencia principal. Es la trazada desde el centro de la hipérbola con radio el semieje real.
-
Circunferencia focal. Al igual que en la elipse existen dos circunferencias focales, una por cada foco. Por lo tanto son circunferencias de centro F o F´ y radio igual a la medida del eje real.
-
Asíntotas. Son las rectas paralelas a la hipérbola, es decir, tangentes a ella en el infinito. Las asíntotas pasan por el centro de la hipérbola y mantienen el mismo ángulo con respecto a los ejes.
|
 |
| Determinación de las asintotas de una hipérbola |
1º Método:
- Para hallar estas rectas, trazamos la circunferencia principal dibujando las rectas tangentes a ella desde el foco. Los puntos de tangencias de esas rectas con la circunferencia, unidos con el centro determinan las asíntotas.
|
2º Método:
- Trazamos una recta paralela por C y por D al eje principal, y por A o B al eje imaginario. Los puntos de corte de estas dos rectas pertenecen a las asíntotas de la hipérbola, por lo que se unen con el centro para dibujarla.
|
|
|
|
| IMPORTANTE: Cuando la longitud del eje real de una hipérbola coincide con la de su eje imaginario, se dice que la hipérbola es equilátera. Por lo tanto las asíntotas son perpendiculares entre sí, formando 45º con los ejes. Por lo que se puede tomar como sistema de referencia, es decir como unos ejes de coordenadas. |
| |
| |
