Hexaedro


HEXAEDRO O CUBO
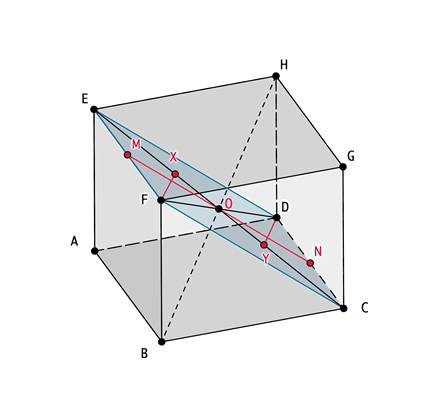
El cubo es un poliedro regular convexo de seis caras cuadradas, ocho vértices y doce aristas. Las diagonales del cubo son iguales y se bisecan en el centro del poliedro, siendo éste su centro geométrico. Al igual que el tetraedro necesita para su represtación, como mínimo, la longitud de su arista. IMPORTANTE: Se dice que dos o más diagonales de una figura o un sólido se bisecan, cuando éstas se cortan en su punto medio.
Sección principal del cubo o hexaedro
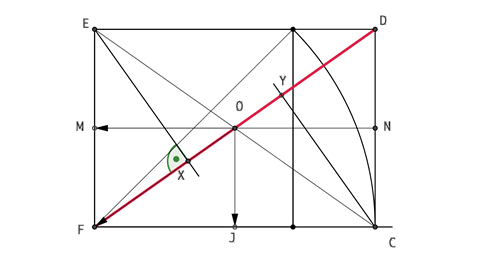
La sección principal del cubo se produce por un plano que contiene a dos aristas opuestas, queda definida por un rectángulo en el que la longitud de los lados menores es igual a la arista del poliedro y la de los lados mayores, a la diagonal de una cara. Elementos que contiene: Arista = EF = CG = a = diámetro de la esfera inscrita Centro del cubo = O, centro geométrico del poliedro Distancia entre aristas opuestas = MN Diagonal de una cara = AC = EG Distancia entre vértices opuestos = FD= EC = diámetro de la esfera circunscrita = Diagonal del cubo 1/3 de la diagonal del cubo = EX = XY = YC = altura de un cubo apoyado en un vértice con su diagonal perpendicular al plano donde se apoya Radio de la circunferencia que contiene tres vértices de aristas concurrentes = XF = DY Rado de la esfera tangente a las aristas=OJ

Cubo con una cara contenida sobre el plano horizontal de proyección
La posición más sencilla a la hora de representar el hexaedro será esta. Al tener sus caras opuestas el hexaedro es un paralelepípedo, cuya proyección horizontal viene dada por un cuadrado, de lado la arista y en proyección vertical un rectángulo de altura, igual a la anterior arista. En proyección horizontal los vértices de la cara superior e inferior quedan confundidos, por pertenecer a una recta vertical.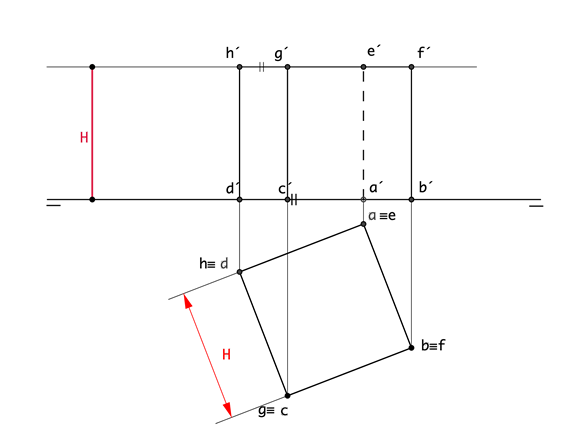
Hexaedro con una arista en el plano horizontal de proyección, manteniendo la opuesta paralela a dicho plano
En este caso el cubo tiene contenido una única arista en el plano horizontal, con lo que, en el sistema diédrico tendrá dos caras proyectantes horizontales y las diagonales de dichas caras serán rectas horizontales. Su proyección horizontal queda definida en un rectángulo de lado menor, la arista y mayor, la diagonal de caras del poliedro. La proyección vertical se consigue trazando líneas auxiliares perpendiculares a la LT. La arista (a´, b´), se deja contenida en la misma LT, por pertenecer al plano horizontal de proyección y los demás puntos se proyectan sobre dos alturas que corresponden, a la de la diagonal completa y a la mitad de ella.
Cubo apoyado en un vértice perpendicular al plano horizontal de proyección

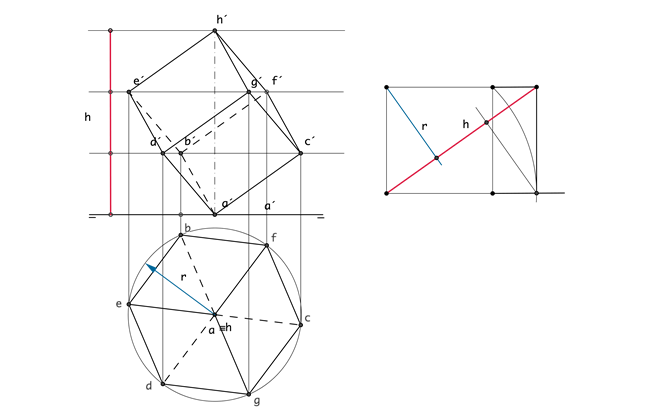RECUERDA: Para conseguir el radio de la circunferencia que contiene tres vértices concurrentes o circunscribe al hexágono (proyección horizontal) basta hacer la media proporcional entre la diagonal del poliedro y un tercio de ésta
Sección por un plano Frontal y verdadera magnitud
El ejercicio planteado esta vez, es el del cubo apoyado sobre su arista en el plano horizontal de proyección cortado por un plano frontal Q. Este caso tiene las mismas caracteristicas que el anterior en cuanto que los puntos de sección son directos. Los puntos de intersección son los puntos de cortes de la traza Q con las aristas en proyección horizontal, en esa proyección la sección está confundida con la traza del plano, por ser paralelo al vertical y perpendicular al horizontal, la proyección de la sección en el vertical sería la resultante de trazar líneas auxiliares perpendiculares a la LT en el corte con la arista correspontiente. La sección se encuentra en verdadera magnitud.
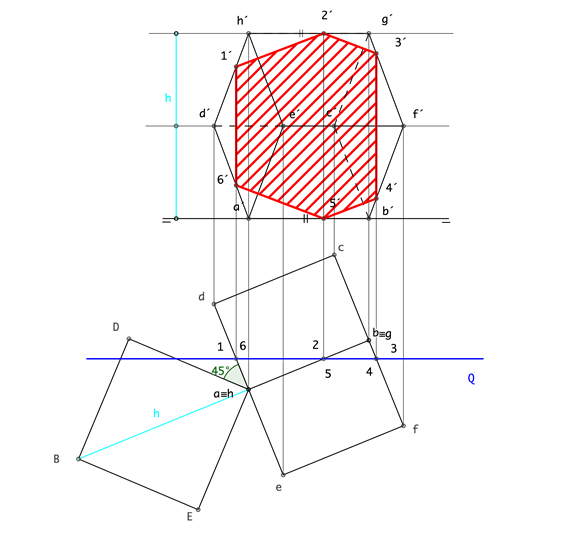RECUERDA: Las secciones están contenidas en los planos y a menos que estos sean paralelos a uno de los planos de proyección su forma no se encuentra en verdadera magnitud, para poder situar la sección en verdadera magnitud es necesario utilizar uno de los métodos estudiados, en estos caso abatiremos hacia el horizontal o el vertical de proyección.
Cubo apoyado en un plano paralelo a la línea de tierra

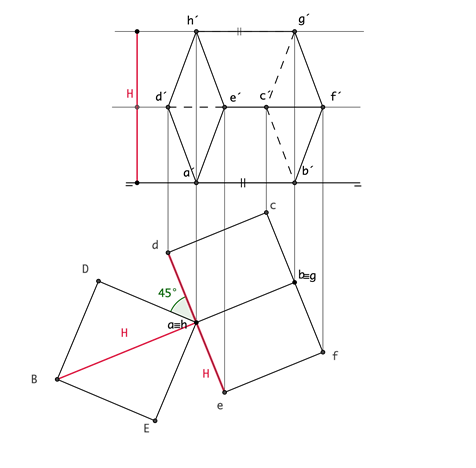
Para dibujar el cubo apoyado en el plano se nos da la diagonal del cuadrado base. Para ello y sabiendo que el plano es paralelo a la línea de tierra se dibuja el plano que contine dicha recta. Se abate la diagonal y se dibuja el cuadrado. Luego se levanta la altura en el perfil.