Tetraedro


TETRAEDRO
El tetraedro es una superficie poliédrica formada por cuatro caras con forma de triángulos equiláteros, seis aristas, y cuatro vértices. Para la representación de este poliedro y de su sección principal, es suficiente con conocer su arista. Las posiciones que vamos a estudiar del tetraedro son tres: apoyado sobre una cara, apoyado sobre una arista siendo su contraria paralela al plano horizontal de proyección y apoyado sobre un vértice perpendicular al plano horizontal de proyección. ATENCIÓN: La construcción de la sección principal nos posibilita el conocimiento de los elementos necesarios para la representación de este sólido, aunque podemos emplear otros procedimientos.
Sección Principal
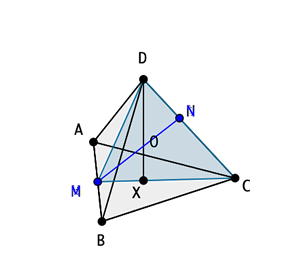
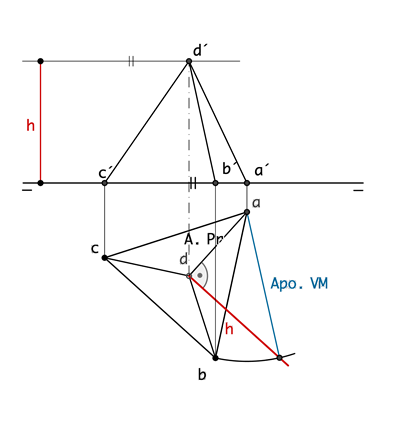
La sección se determina por un triángulo isósceles MCD, resultante del corte del tetraedro por un plano que pasa por una arista y la altura de la cara opuesta a ella. (fig.1) Elementos que contiene: Arista = DC = a Centro del tetraedro y ortocentro = O Altura del tetraedro = DX = h Altura de cara =MC = MD Ángulo formado por dos caras consecutivas = CBM Distancia entre aristas opuestas = MN Radio de la esfera inscrita = OX Radio de la esfera circunscrita = OD

Tetraedro con una cara sobre el plano horizontal de proyección
¿SABÍAS QUE...? … la altura de un tetraedro es un cateto de un triángulo rectángulo en el que el otro cateto es 2/3 de la altura de una cara y la hipotenusa es la arista? La proyección horizontal estará representada por un triángulo equilátero (A, B, C) de lado el tamaño de la arista en verdadera magnitud. El vértice opuesto equivale en proyección vertical a la altura del sólido, este se sitúa en el centro del triángulo. La proyección vertical se obtiene refiriendo los vértices A, B, C sobre la LT y la del vértice D se obtiene al hallar su cota ya sea por la sección principal o por la teoría del triángulo rectángulo mencionado anteriormente. Uniendo estos puntos obtenemos el contorno aparente del tetraedro RECUERDA: Todos los puntos contenidos en alguno de los planos de proyección tienen una proyección coincidente con el punto del espacio y la otra contenida en la línea de tierra.
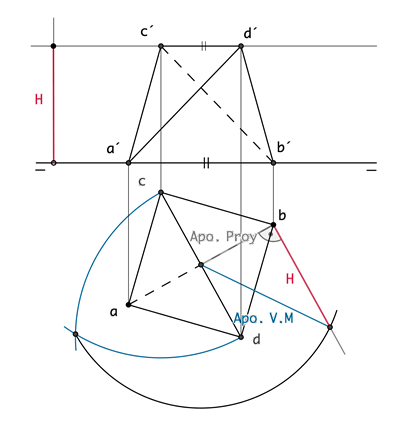
Tetraedro apoyado sobre una de sus aristas contenidas en el plano horizontal de proyección, estando la opuesta paralela a este.
Una de las propiedades geométricas de tetraedro es, que sus aristas se cruzan, dos a dos, perpendicularmente. Teniendo esto en cuenta, la proyección horizontal del tetraedro estará formada por un cuadrado cuyas diagonales son las aristas mencionadas anteriormente. Por estar una de ellas contenida y la otra paralela se encuentran en verdadera magnitud. Para obtener la proyección vertical tendremos que llevar sobre la línea de tierra la mínima distancia entre aristas opuestas que se halla por la sección principal o abatiendo en el horizontal esta magnitud. ¿SABÍAS QUE?... …La mínima distancia entre aristas opuestas es un cateto, de un triángulo rectángulo en el que la hipotenusa es la apotema en verdadera magnitud y el otro cateto la proyección de ésta.
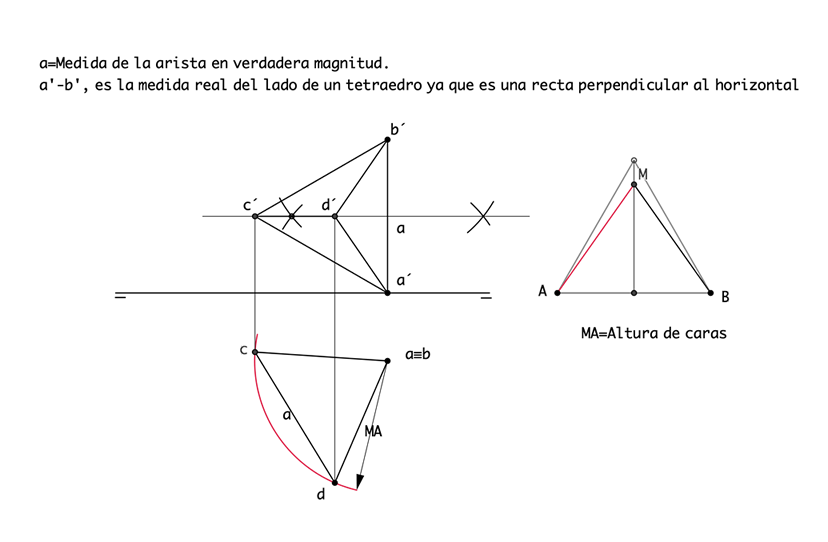
Tetraedro apoyado en un vértice con una arista perpendicular al plano horizontal de proyección
Tanto la proyección horizontal como la vertical son triángulos. La arista perpendicular es una recta vertical por lo que dos de los vértices del tetraedro están coincidentes es su traza horizontal. La proyección horizontal se obtiene haciendo una circunferencia con centro en la traza horizontal de la recta y radio la altura de caras, sobre este arco se sitúa la arista en verdadera magnitud del tetraedro. En proyección vertical basta trazar la mediatriz del segmento que forma los vértices a´ y b´ y proyectar sobre esta recta los restantes vértices del sólido. Para averiguar la altura de caras nos auxiliaremos de la sección principal.

Sección por un plano proyectante vertical y verdadera magnitud
El poliedro excogido es el tetraedro con una cara contenida en el plano horizontal de proyección y el plano secante, P (P´-P) de canto. Este ejercico no requiere dificultad alguna, ya que el plano es perpendicular al vertical con lo que los puntos de corte de la traza vertical del plano con las aristas del tetraedro son los puntos de intersección, queda referir estos puntos sobre las aristas en proyección horizontal y abatir la sección para obtener su verdadera magnitud
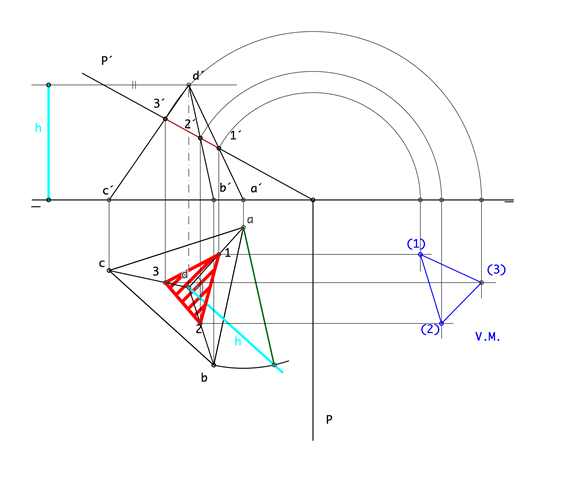RECUERDA: Las secciones están contenidas en los planos y a menos que estos sean paralelos a uno de los planos de proyección su forma no se encuentra en verdadera magnitud, para poder situar la sección en verdadera magnitud es necesario utilizar uno de los métodos estudiados, en estos caso abatiremos hacia el horizontal o el vertical de proyección.
Sección y verdadera magnitud de un tetraedro con un plano paralelo a la línea de tierra

1º Debemos hallar el plano sabiendo que está formado por dos rectas que se cortan. 2º Como el tetraedro tiene una de sus caras contenidas en el plano horizontal de proyección, dibujamos su base (triángulo equilátero) y hallamos su altura. 3º Procedemos a seccionar. Como el plano que hemos obtenido en el primer apartado es paralelo a la línea de tierra, es más sencillo hallar su intersección en el perfil. 4º Por último abatimos la sección.