| OCTAEDRO | |
Es uno de los cinco poliedros platónicos formado por ocho caras que son triángulos equiláteros, doce aristas y seis vértices. Sus tres diagonales son iguales, perpendiculares entre si y se bisecan. Hay que tener en cuenta que sus caras opuestas son paralelas dos a dos y al igual que los poliedros anteriores sólo se necesita el conocimiento de su arista para su construcción. |
|
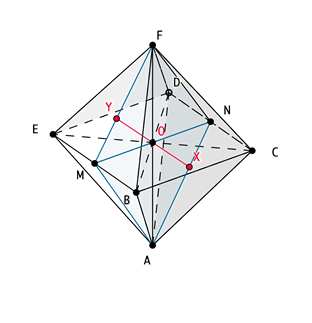
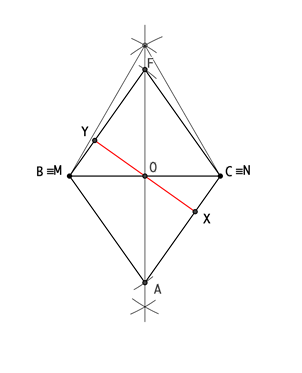
| Sección principal | |
En el octaedro, esta sección esta producida por un plano secante que contiene dos vértices opuesto y pasa por la mitad de dos arista. La figura surgida de esta sección es un rombo, cuyos lados son las atura de caras del poliedro y sus diagonales la distancia entre vértices opuestos y la arista del mismo Elementos que contiene:
|
|
  |
|
| Octaedro apoyado sobre un vértice teniendo una diagonal perpendicular al plano horizontal de proyección | |
Ya que el octaedro tiene una diagonal dispuesta de forma vertical, su plano medio será paralelo al plano horizontal y contiene a los vértices B, C, D, E. Con lo que en proyección horizontal su contorno aparente es un cuadrado de lado igual a la arista y vértices b, c, d, e. Las aristas laterales del poliedro se representan en proyección horizontal confundidas con las diagonales de este cuadrado cortándose en su punto medio en los vértices a y f. Si observamos esta proyección se ven las cuatro caras superiores del octaedro, las otras cuatros se encuentra por debajo y coincidentes con las superiores. La proyección vertical se define al referir los puntos del plano medio hasta un plano horizontal de altura la mitad de la diagonal, el vértice a´ se contiene en la LT por ser éste el de apoyo del octaedro y el vértice contrario f´ se dibuja con cota igual a la diagonal del octaedro. Uniendo estos puntos obtenemos la representación diédrica del sólido. |
 |
| Octaedro con una cara contenida en el plano horizontal del proyección | |
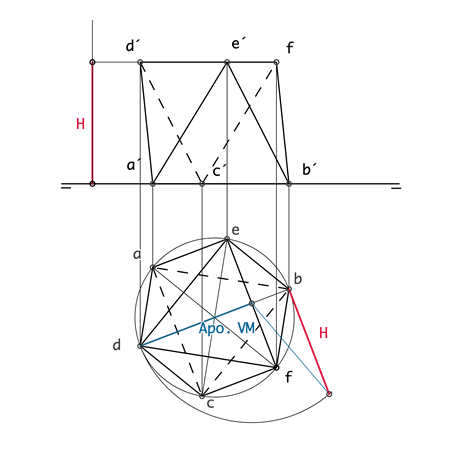
El contorno aparente en proyección horizontal es un hexágono regular, formado por dos triángulos equiláteros que se ha girado uno del otro 180º, la longitud del lado del triángulo es igual a la arista del poliedro, ya que estas son la cara superior e inferior del mismo y por estar una contenida y la otra paralela al plano horizontal de proyección se disponen en verdadera magnitud. Esta representación se puede dibujar según una circunferencia de radio YF (circunferencia que contiene tres vértices del poliedro) La proyección vertical se dibuja separando estas dos caras una distancia igual a la que hay entre caras opuestas, hallada en la sección principal o por medio de abatimiento. ¿SABÍAS QUE... … la distancia entre caras opuestas es un cateto de un triángulo rectángulo en el que la hipotenusa es la altura de caras en verdadera magnitud y el otro cateto la proyección de la misma? |
 |
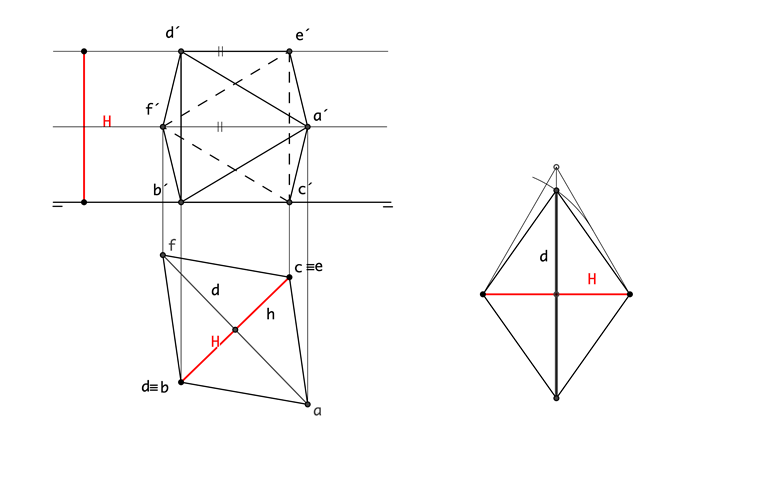
| Octaedro con una arista en el plano horizontal de proyección, manteniendo la otra paralela a dicho plano | |
La proyección horizontal del octaedro es igual al rombo descrito en la sección principal y su alzado queda determinado al llevar sobre dos alturas los vértices, una de ellas es la arista en verdadera magnitud la otra la mitad de esa arista. Los vértices contenidos en el plano horizontal de proyección se dibujan en proyección vertical sobre la LT formando una recta horizontal al igual que la arista paralela a ella. |
|
 |
|
| Sección por un plano palaralelo a la L.T. y verdadera magnitud | |
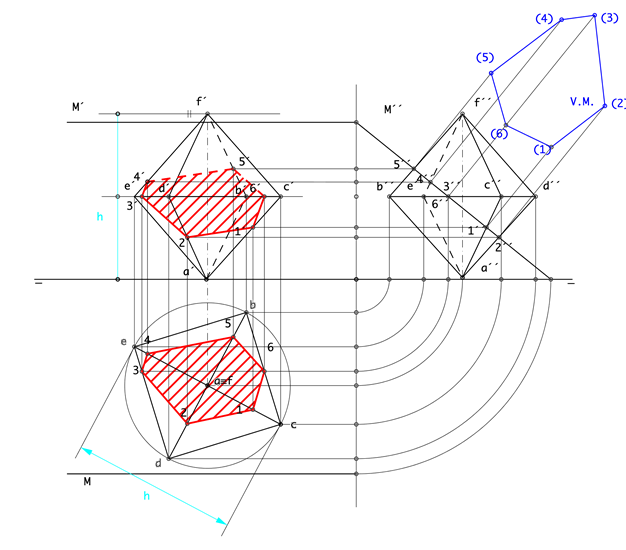
Dado el octaedro con un vértice en el horizontal de proyección, siendo la diagonal que parte de este vértice vertical y el plano M (M´-M) paralelo a la LT, procederemos según uno de estos casos:
Para facilitar la realización del ejercicio lo resolveremos utilizando el plano de perfil ya que los puntos de sección son directos en esa posición, basta llevarlos tanto al vertical como al horizontal y luego hallar la verdadera magnitud de la sección, como se aprecia en la imagen. |
|
 |
|
RECUERDA: Las secciones están contenidas en los planos y a menos que estos sean paralelos a uno de los planos de proyección su forma no se encuentra en verdadera magnitud, para poder situar la sección en verdadera magnitud es necesario utilizar uno de los métodos estudiados, en estos caso abatiremos hacia el horizontal o el vertical de proyección. |
|
| Sección y verdadera magnitud de un octaedro por un plano que corta o contiene a la LT | |
En este caso se da un octaedro apoyado en uno de sus vértices perpendiculares al plano horizontal de proyección y el plano que corta al octaedro pasa por su centro y contiene a la línea de tierra. En este caso primero debemos dibujar la proyección vertical del octaedro sabiendo que todas las diagonales miden lo mismo, luego el plano y posteriormente la sección que será directa en el perfil.
|
|