| SISTEMA DIÉDRICO: PERPENDICULARIDAD | |
| La perpendicularidad entre rectas, planos o entre recta y plano no se manifiesta directamente en las proyecciones diédricas de estos elementos, sino en posiciones particulares. | |
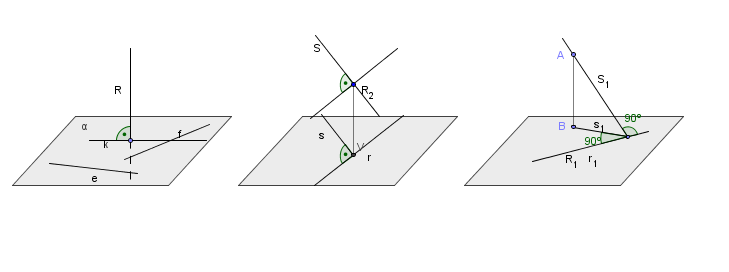
| Axiomas de la perpendicularidad 1º Axioma. Toda recta perpendicular a un plano lo será a las infinitas rectas contenidas en dicho plano, se muestren estas o no perpendiculares en proyección. Para poder demostrar que la recta es perependicular a un plano, es necesario que sea perpendicular a dos cualesquiera de ese plano mientras que no sean paralelas. 2º Axioma. (teorema de las tres perpendiculares) Si dos rectas del espacio (R) y (S) son perpendiculares y una de ellas, la (R) es paralela a un plano, las proyecciones ortogonales (r) y (s), de las dos rectas sobre este plano serán también perpendiculares. Y viceversa, si las proyecciones (r) y (s) de dos rectas (R) y (S) del espacio son perpendiculares, y una de ellas es paralela al plano de proyección, ambas rectas serán perpendiculares en el espacio. Por el punto de intersección de las dos rectas, se pueden pasar infinitas rectas perpendiculares a la recta (R); y que definirá un plano perpendicular a ella. A su vez como (R) es paralela al plano el plano que define (S) será perpendicular al de proyección, es decir, es proyectante al plano y su traza la proyección (s). 3º Axioma. Un caso particular del teorema de las tres perpendiculares es cuando la recta que es paralela al plano se encuentra contendida en él, con lo que si una recta es perpendicular a una recta cualquiera del plano, su proyección ortogonal sobre este plano también será perpendicular. Si por el pie de una perpendicular a un plano se traza una recta perpendicular a una recta contenida en dicho plano, la recta que va desde el punto de corte de esa recta con la que estaba en el plano hasta un punto cualquiera de la perpendicular al plano es también perpendicular a la recta que estaba sobre el plano. |
|
|
|
| RECTAS PERPENDICULARES ENTRE SÍ | |
| Recta
perpendicular a otra por un punto contenido en la recta Recordando el teorema de las tres perpendiculares, si una de las rectas es paralela a un plano sus proyecciones se mostrarán perpendiculares sobre dicho plano; por lo tanto si la recta se sitúa paralela, a alguno de los planos de proyección, la perpendicularidad entre las dos rectas se verá sobre el plano de proyección al que dicha recta es paralela, es decir, si una de las rectas es frontal, las proyecciones de dicha rectas sobre el vertical serán ortogonales, y viceversa. |
|
|
|
| Recta
perpendicular a otra por un punto exterior a la recta Como se dijo en un principio toda recta perpendicular a un plano, lo es a las infinitas rectas contenidas en él, se corten o no en su punto de intersección y viceversa todas las rectas contenidas en un plano perpendicular a una recta dada, lo es a la recta dada, pase por su punto de interesección o no. Con lo que el ejercicio queda resuelto al trazar un plano que sea perpendicular a la recta dada; siendo todas las rectas contenidas en él directamente perpendiculares a la recta dada. |
|
|
|
| Infinitas rectas perpendiculares a una recta dada | |
| Cualquier recta que esté contenida en un plano perpendicular a la recta dada será perpendicular a dicha recta. | |